Abstract:
The Expressway method is a new method for understanding and manipulating pointers. It does a sort of deskilling job for the programmers. It is easy to understand because it corresponds to a real life analogy. People can evaluate and also make their own pointer expressions quite easily. Since the method is mechanical, chances of errors and mistakes are minimized and you would not get messages like “bad pointer”, “invalid indirection”, “non portable pointer conversion” etc. The only things you need to know are the traffic rules. The method makes a nice analogy between the memory locations and the expressway and uses this analogy to solve pointer expressions.
The Analogy
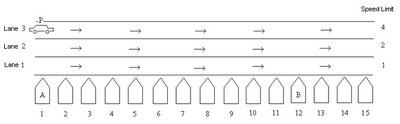
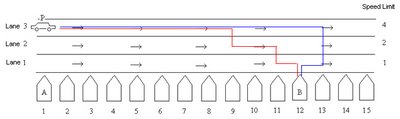
Suppose we all live in a small colony where all houses are lined up in a row as shown in the diagram 1. We have an expressway just beside the colony as shown in the Figure 1 (only one way of the expressway has been shown for convenience). Now as with a usual expressway we also have traffic rules here. It’s a three lane expressway and the innermost lane from the above (Lane 3) is for high speed vehicles and the outermost (Lane 1) is for slow vehicles. As shown in the diagram I have used numbers to indicate the speed limits of the different lanes. The lane 1 has a speed limit of one speed unit. Assume speed unit as a basic speed of which all other are multiples. The next lane (Lane 2) has the speed limit double of the first lane. And similarly lane 3 has speed limit that is double of the second lane. We also assume that in a particular lane you can travel by that speed only.
Now suppose a person ‘A’ living in the first house wishes to visit his friend B who lives in the 12th house for tea. He takes out his car and drives to his friend’s house. Let’s assume that he starts from the innermost lane (Lane 3) of the expressway moves 2 units of distance (assume a distance unit as equal to the speed unit for that lane. So Total Distance = Distance Units x Speed Unit, i.e., 2 X 4 = 8) in that lane and reaches house num
ber 9 (his house 1 + 8). Now if he continues in that lane he will surpass his friend’s house (9 + 4 = 13), although he can make a u-turn and come back but here we consider that he shifts the lane. So he follows the traffic rules, and puts on the right indicator of his car and moves to the next lane (Lane 2). In this lane the speed limit is 2 speed u
nits so he travels 1 unit of distance in this lane (1 X 2) and reaches house number 11 (9 + 2). Again he switches his right indicator to move to the outermost lane (Lane 1) which has a speed limit of 1 unit. He then travels a distance of 1 unit (1 X 1) in this lane to reach his friend’s house (11 + 1). The person A has now reached his friend’s house but he is still on the road. So he again switches on his right indicator to move from the road into the house and park the car. This is the general scenario that we all follow to do the same. Figure 2 indicates this and the case where we may surpass the house and take a u-turn.
The Method
The memory of our computer is exactly like the colony discussed above. Irrespective of how many dimensions you use for the array, your data will always be stored sequentially in a line (for contiguously allocated memory). It is of course that you may move here to there using the pointers.
We can consider the data in the memory as the houses of our above example. The memory address of these data items are like the street address of the houses in the above example. The number of lanes in the expressway equals the number of dimensions we use to store the data in the memory. While taking a right turn in our example we switched on the right indicator, here we use the indirection operator ‘*’ (asterisk) to indicate a right turn. And similarly for the left turn we use the address operator ‘&’ (ampersand). Now a question arises that how do we set the speed limits of the individual lanes? The speed limits of the lanes are set according to the size of that dimension (array size).
Let us suppose that we have an array declared as:
array[P][Q][R]; (Listing 1)
Then we will create a three lane expressway because the array is three dimensional. The first lane (from below) or the outermost lane will always have the speed limit of 1 unit. The next lane will have the speed limit of (R x 1). For the next lane the speed limit will be (Q x R x 1) and so on. Once we have set the speed limits of all the lanes we are ready to build our pointer expression.
The pointer expression will always start with the array or the pointer name so we write the name of the array or pointer. Next as in the case of our colony example we will start from the innermost lane (from the above). Now you have to calculate the distance units (distance units = total distance traveled / speed of the lane) that you can travel in that lane so as to reach nearest to your destination. Once you get the distance units, add that number to the array or pointer name. If the number of units is ‘i’, you will get this:
array + i (Listing 2)
Now if you have to change the lanes - for this put the entire expression in parentheses and add the indirection operator to the left of the expression. You will get,
*(array + i) (Listing 3)
Now if you need to travel more in that lane, add the number of unit distances traveled in that lane to the right of the expression. While changing lane to the right put the entire expression in parentheses and add the indirection operator to its left. You can also travel backwards like taking a u-turn. For this you should subtract the distance unit traveled in the opposite direction. For taking a left turn you should put the entire expression in parentheses, and put the address operator ‘&’ to the left of the expression.
To get the address of the data item multiply the total distance traveled, by the size of the data type and add it to the starting address of the pointer. Suppose the starting address of the array is ‘A’ and you traveled a distance of ‘B’ then your current memory address location will be;
A + (B x Size of the data type) (Listing 4)
Now, given a pointer expression, you can also find out the data or memory location using the same principles.
Example 1
Given an array a[2][3][4] you need find an expression to get the 22nd element.
int ***p = a;
Solution:
The expressway will be of three lanes as we have a three dimensional array. You can draw it on paper.
The speed limit of the first or outermost lane (Lane 1) will be 1.
The speed limit of the second lane (Lane 2)will be 4 (4 x 1)
The speed limit of the innermost lane (Lane3) will be 12 ( 3 x 4 x 1)
Start the expression with the name of the pointer i.e., p
We start with the lane 3 and we can travel only one distance unit (12) in that lane to reach at element 13 (starting position + distance). Our expression becomes p + 1
We need to shift the lane to the right, i.e., put parentheses and the indirection operator. Our expression becomes *(p + 1)
In the second lane we can travel two distance units (2 x 4) to reach element 21 (13 + 8). Our expression becomes *(p + 1) + 2
We shift the lane to the right. Our expression becomes *( *(p + 1) + 2)
We move one distance unit in the outermost lane to reach element 22 (21 + 1). Our expression becomes *( *(p + 1) + 2) + 1
Although we have reached the desired element, we are still on the road / memory address. To get the data at this location we need one more right turn. Our final expression becomes *( *( *(p + 1) + 2) + 1)
Assuming p starts at memory location 1000, the memory address of this data item is 1042=1000 + ((22 -1) x 2) i.e., (starting address + distance traveled x size of data type) for a 16 bit compiler
Example 2
Given the array
int p[3][3][3] ;
Find the value of expression; *( *(p + 2)) +2
Assuming a starting address of 1000 and a 16 bit compiler.
Solution:
The expressway will have three lanes
The first or outermost lane (lane 1) will have the speed limit of 1
The second lane will have a speed limit of 3 (3 x 1)
The third lane will have a speed limit of 9 (3 x 3 x 1)
Starting from the innermost lane (Lane 3) location 1, we will travel a distance of 18 (9 x 2) to reach at location 19 (18 + 1)
We find an indirection operator so we move right to the second lane
Again we find the indirection operator so we move right to the first lane
We travel in this lane a distance of 2 (1 x 2) to reach location 21 (19 +2)
The expression ends; but we are still on the road / memory location. So the output memory address i.e., 1040 = 1000 + ((21 – 1) x 2)